Parabolic Pitch

Sports are boring. We need something new. I present Barf Ball, conceived during a mechanics course in undergrad.

Sport Played in a Rotating Parabolic Dish

The sport takes advantage of the unusual phenomena that occur in rotating frames of reference, much in the same way as a game played in space would introduce a new kinematic experience like the zero-gravity game played in "Ender's Game."

The sport is played on a rotating parabolic pitch with a radius of as much as 30 meters. The pitch should be fully enclosed, and all lighting and cameras should be in the rotating frame to ensure complete absorption in the new reality of the rotating frame. Rotation is set to roughly one revolution every 5 to 10 seconds, and the parabolic shape is defined to achieve a perpendicular apparent gravity at all points on the surface. This means you can stand anywhere in the bowl. And when you look up, you can see someone else standing on the ceiling.

Figure 1. Stand normally anywhere in the bowl.

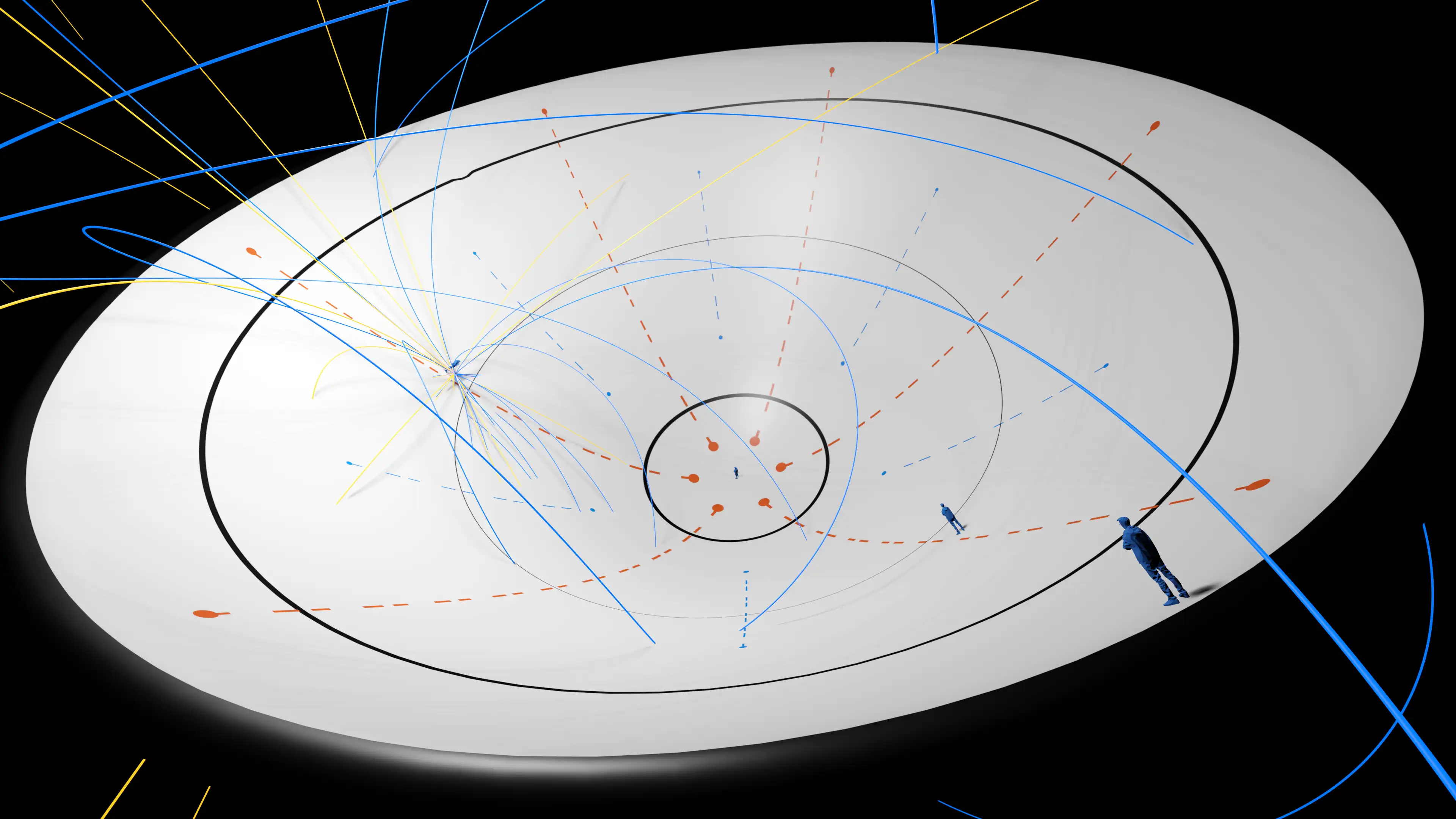
Phenomena

The game contains many physically unusual aspects arising from rotary motion - more than can properly be predicted without actually experiencing such a pitch. The following is a brief description of expected phenomena. It may be helpful to watch this explanation from 1960's University of Toronto.

The basic idea is that in 0 gravity, objects travel in straight lines. When you add gravity, objects travel in parabolas. When viewed from above, parabolas are just straight lines, like the yellow lines below. And finally, when you look at parabolas from a rotating frame, which is what we're doing in the bowl, they look wonky like the blue lines.

Figure 2. A random set of simulated trajectories for fixed (yellow) and rotating (blue) frames of reference.

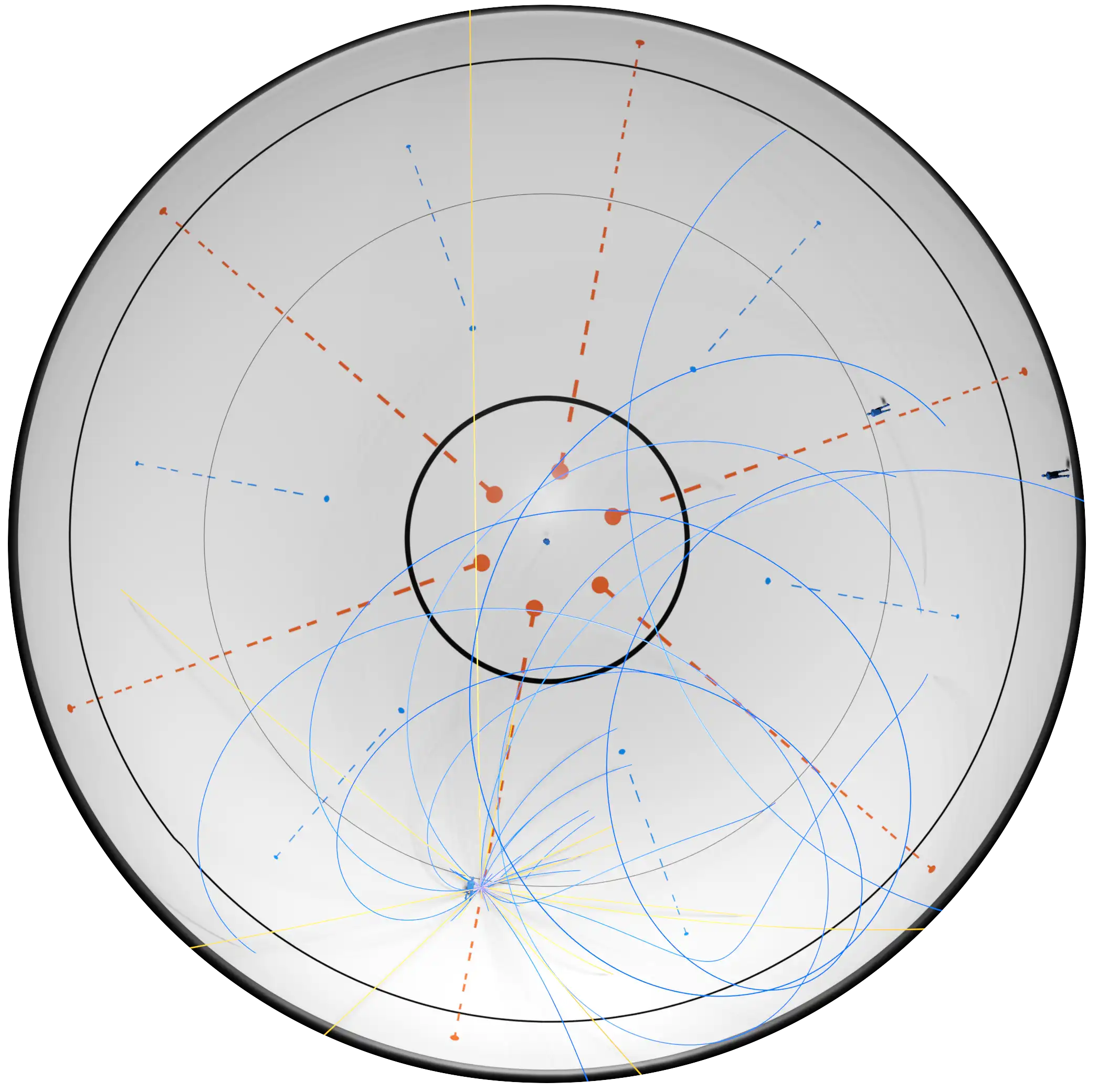
The centrifugal force increases linearly with increasing radius. But the design of the pitch is such that the centrifugal force and Earth’s gravity combine for an effective gravity that is perpendicular to the surface at all points on the pitch meaning a ball at rest will remain at rest in the rotating frame. This is in contrast to a flat rotating pitch where the ball will roll outwards and opposite to the rotation. This is only true for a ball on the surface. Above the surface, a ball at rest will go outwards and down. The effective gravity increases going out from the center. Players will feel 1-2 times heavier depending on where they are on the pitch. Their bodies will be savagely overused in the high gravity outer regions and there is danger in prolonged stay.

In a non-rotating environment, the ball follows air dampened parabolic trajectories. But on a rotating pitch, the motion of the ball will be subject to Coriolis and centrifugal forces making the trajectories depend on direction, position, and velocity of the throw. In general, tangential passes in the direction of rotation will skew outwards while tangential passes opposite the direction of rotation will skew (or spiral) inwards. Passes towards the center will skew in the direction of rotation, while outward passes will skew against the rotation. Everything falls to pieces when one considers bounces and spin which will flip each time the ball crosses the court. Clearly, the perceived physics is changed and rather more complex than what we are used to, yet still predictable and open to manipulation for cunning athletes.

Figure 3. Same set of trajectories for fixed (yellow) and rotating (blue) frames of reference.

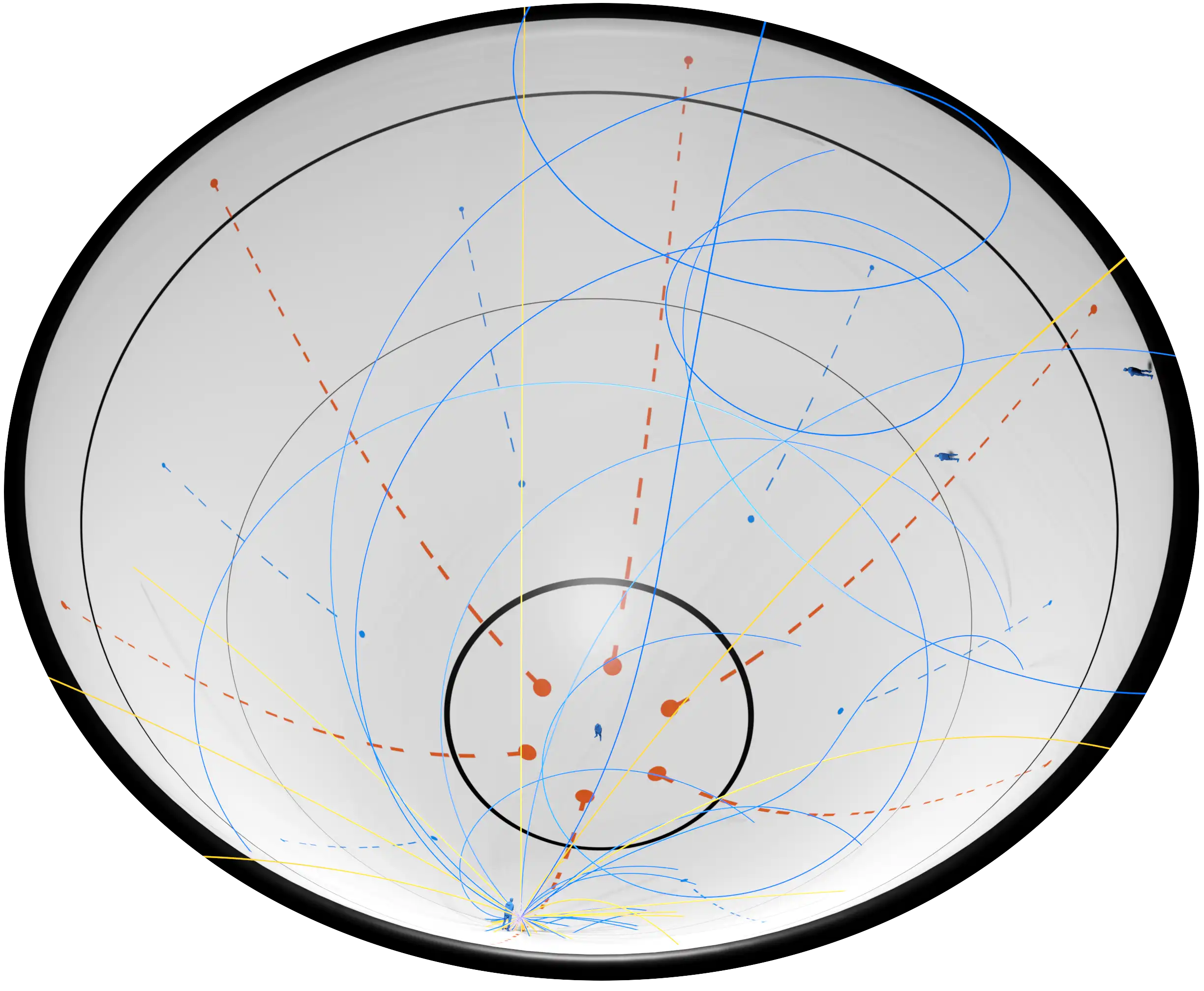
Standing will be simple, though with additional artificial weight and a bit of nausea. Running will be complicated. The same forces that affect ball trajectories are felt by the runner during each foot to foot trajectory. How will he choose his path? Will he run at a slant? Will he notice differential centrifugal forces on his body? How will he avoid slipping on the barf slicked pitch? Only a complete and functioning prototype of the Barf Ball pitch can effectively answer these questions.

Possible Rules

The game might be structured like Rugby. There is a central disk, the speed disk, with 5 meter radius in which gravity is pretty much normal. The outer ring, the slow ring, with 5 meter width has a 1.5x greater gravity. The ball can be handled in any way. The game begins with the ball dropped centrally (it spirals down if dropped slightly off center from the Earth frame), with all players outside of the speed disk. Once the ball touches the pitch, players can enter the speed disk to contest initial possession. The ball must go from speed disk to slow ring and back to the speed disk in continuous possession to score a point, which does not reset possession or bring the game to any kind of pause. Barring fouls, gameplay is continuous during the two, twenty minute oppositely rotating halves. The sport is contact in the same way soccer or basketball is contact. There are fouls for excessive physicality, elbow poking, and foot kicking. Fouls lead to change in possession at the location of the foul, with the offender having to start from the slow ring once gameplay recommences.

Pitch Control

In operating the pitch, we have the option of applying a torque to conserve either rotation rate or energy. If we conserve rotation rate, the torque applied will counteract any changes in the moment of inertia and rotation rate will be constant. If we conserve energy, the distribution of mass on the rotating pitch will determine its moment of inertia, which then sets the rotation rate. Just as an ice skater will pull in her arms for faster rotation, players could shift to the middle of the pitch to increase rotation or vice versa depending on strategic merit. I can imagine one team clustering to the center while the other team is in the slow ring in order to increase rotations and make the journey from the outer ring more strenuous or even impossible. This facet of the game would require that the player’s weight has a significant effect on the moment of inertia, which means the pitch would need to be very light. Even so, the torque could be computer adjusted to amplify the rotational effects of changes in the moment of inertia so that even a small change in the moment of inertia could significantly change the rotation rate.

Demonstration?

Barf Ball facilities would be expensive. Cost estimates might be based on rotating platforms used for carnival rides, radars, or fatigue carousels.

Conclusion

This game is uniquely difficult as it forces players to redefine their physical intuition - an intuition shaped by years of living in a negligibly rotating environment. Players need to be pretty clever to make position and speed dependent decisions. And they need to be pretty athletic to deal with the extra gravity and high impact falls.

A sport must simulate war, require both strength and cunning, and most importantly, provide the masses with glorious spectacle. Barf Ball is sport to an unprecedented degree. It is more warlike than football due to the overabundance of variables and physical hardship. It requires unearthly feats of strength and cunning unmatched in any other sport. And it is pure spectacle with gut-churning novelty and a beautifully unfamiliar physics.

---

Pitch Dimensions

Figure 2. Barf Ball pitch dimensions .

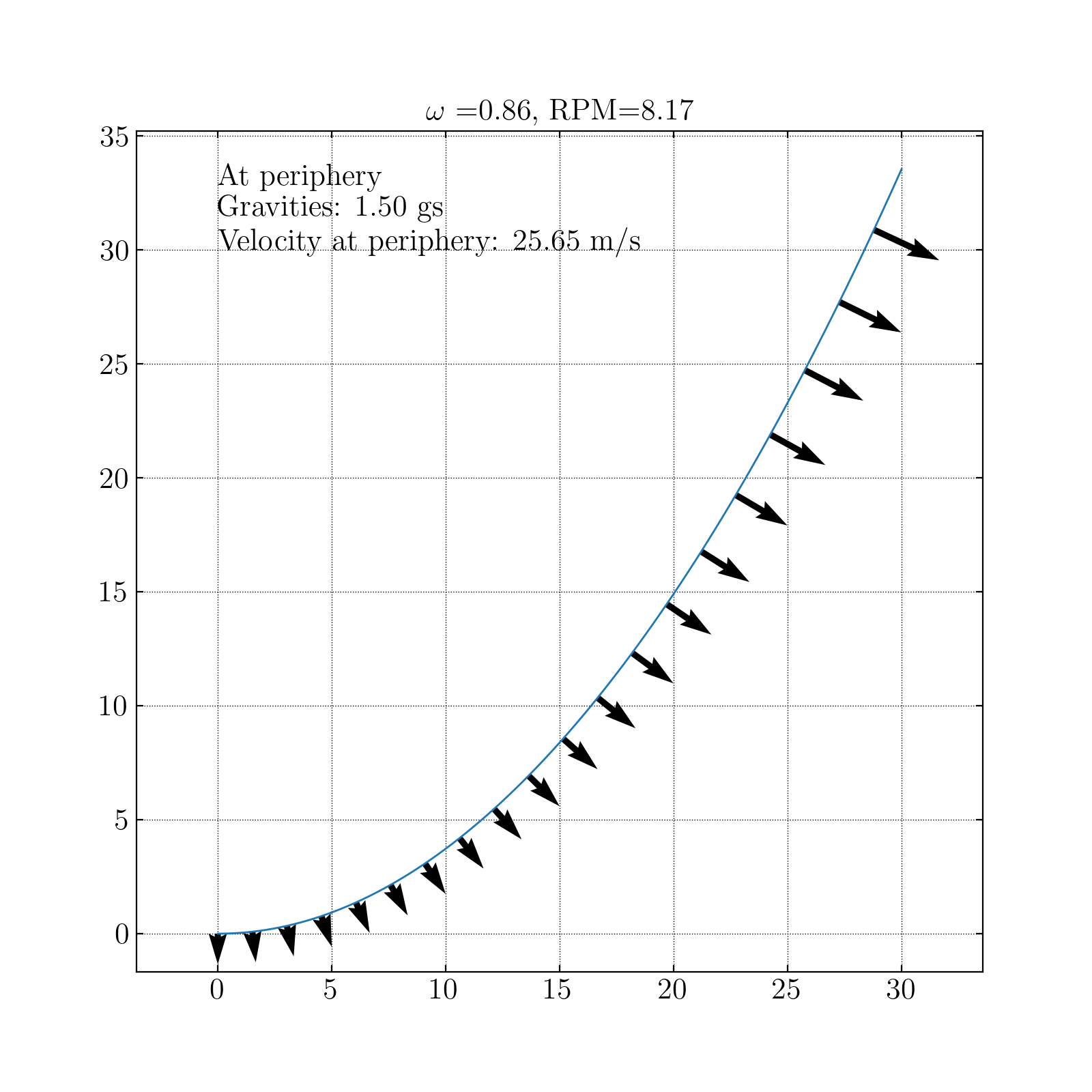
The dimensions of the pitch are defined to achieve an effective force that is perpendicular at all points on the surface, and therefore depends on the rotation rate.

The effective gravity as a function of radius is just the vectpr sum of the centrifugal acceleration and the gravity and has magnitude

$$g_{eff} = \sqrt{ \frac{\omega^{4} r^{2}}{4}+ g^{2}}$$

We rearrange to find the rotation rate as a function of desired periphery gravity,

$$\omega = \frac{(g_{eff}^{2} -g^{2})^{\frac{1}{4}}}{\sqrt{r/2}}$$

To achieve 1.5 gravities at a radius of 30 m requires 8.17 rotations per minute.

The surface of the pitch is defined by equating the taking the inverse of the normal force as the slope, and integrating.

$$(r,z) = (r,\frac{ \omega^2 r^2}{2g})$$

For a 1.5 g effective gravity at 30 meter radius, the pitch will be 35 meters in height.

---

First wrote in 2015. Edited in 2022.