Cookie Dunking Phenomena and Design (Part 1)

Previously, Len Fisher addressed the issue of biscuits lost at tea ¹. As a cookie soaks, the sugar and fats dissolve, the starch grains bloat, and the biscuit falls apart pretty quickly. Fisher was trying to increase the dunk time before structural failure so the timing would be less stressful and finicky. The strategy he proposed was:

1. Insert one end of the biscuit into the liquid at an angle which can lead to a dryer structural top side (his explanation) for longer; and
2. Add a chocolate sheet that keeps it structurally sound.

He won an (Ig) Nobel Prize for this. But the "horizontal" orientation offers such a small advantage that he has to use a supersize cookie for demos and the results look insubstantial in practice. The angling has not really done it for me. The wet front climbs the cookie without leaving much of a dry side.

In any case, I have a different problem because I like to soak cookies in whole milk which, as I’ll explain later, is a painfully slow process with mixed results. For example, the cookie can equilibrate with a dry portion inside depending on how it is dipped. I just want to wolf down fully soaked cookies as fast as possible but without losing them. I'm also interested in a cookie I can just toss in and wait to see it soak without sinking. The general strategies are listed below, and they will make sense using a simple equation and a few other observations.

1. Minimize soak path length.
2. Orient horizontally to reduce the gravitational head or submerge partially so that gravity pushes liquid into the cookie from above.
3. Maximize the wetted surface for a larger flow area with geometries of high surface area to volume ratio.
4. Maintain a snorkel to allow gas to escape. Without a snorkel, the gas may become trapped.
5. Use chocolate for water impervious structure but also to create dynamic gas traps.
6. Increase pore size and surface tension.
7. Reduce liquid contact angle (highly wetting) or control for desired function.
8. Keep in mind the shortest path length, and use shapes that have a single path length - torus, sphere - so things don't snap off.
9. Use surface tension to keep soaked objects afloat.

What is soaking?

Soaking a cookie involves a liquid displacing the air in the cookie’s porous interior. Why is this even possible? Hydrostatic pressure and capillary rise of the fluid can drive the fluid to displace the air. Hydrostatic pressure is just the phenomenon that liquid will fill the cavities up to the liquid surface, like an inverted cup in water. Capillary action is what pulls liquids up thin tubes.

We can think of the cookie and its pores as a network of capillaries that feed up and sideways, and we just fit the observed data to find equivalent radii and contact angles that work. One picture is a capillary going up the cookie. We might also consider the capillaries in the short direction.

1 Network of capillaries to approx a cookie.

To account for the many pores that interface with the liquid surface, we can simply multiply by the wetted surface area. Cookie porosity is in the range of 0.5 to 0.8 ². Pore size ranges from 5 to 300 microns, and a representative pore size would be about 150 microns ³.

Capillary rise, also called imbibition, pulls the fluid to rise above the liquid surface level until this capillary pressure balances with the pressure of the liquid column. Balancing the two pressures gives the following equilibrium soak distance $X$ along the cookie where $H$ is the height, $\alpha$ is the angle of the column with respect to the surface, $\theta$ is the liquid contact angle of the fluid, $\sigma$ is the surface tension, $r$ is pore radius, and $\rho$ is the density. This is also known as Jurin’s Law.

$$X = \frac{H}{\sin{\alpha}} = \frac{P_{\text{cap}}}{P_{\text{grav}}} = \frac{\frac{2\sigma\, \cos\left(\theta\right) }{r}}{\rho g\, \sin\left(\alpha\right)}$$

2 Slanted capillary tube.

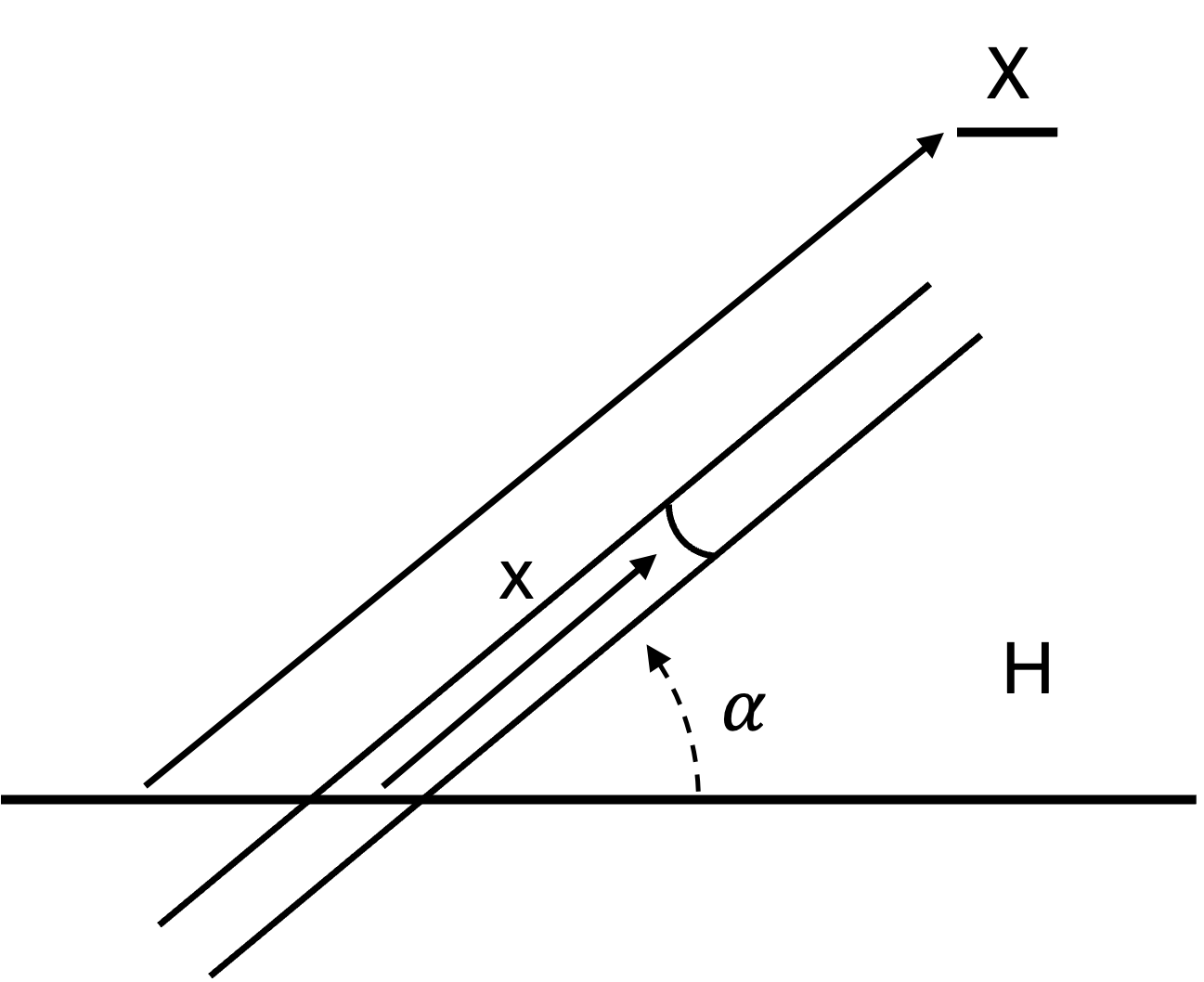
As it happens, this equilibrium soak length is often very large, much larger than a cookie. So we’re actually interested in the velocity or soak rate to achieve a certain $x$ soak length rather than the max equilibrium soak length $X$. To do that, we use the Hagen–Poiseuille equation which describes laminar flow for incompressible Newtonian fluids.

Starting from the Hagen–Poiseuille equation we have

$$\frac{dx}{dt} = \frac{r^2}{8\mu x} \Delta p$$

The pressure term is the capillary pressure minus the column pressure. For areas under the liquid surface, there is an additional but negligible pressure of the liquid height which is ignored here.

$$\Delta p = \Delta p_C + \Delta p_{h} = \frac{2\sigma\, \cos\left(\theta_s\right)}{r} - \rho g x \sin\left( \alpha\right)$$

Substituting into the above velocity equation

$$\frac{dx}{dt} = \frac{r^2}{8\mu} \left[ \frac{2\sigma\, \cos\left(\theta\right)}{r x} - \rho g \sin\left(\alpha\right) \right]$$

Already this shows how reducing the angle of the cookie can increase the velocity along the cookie length. I think Fisher's idea was that this is a small effect and one can increase the soak along the cookie to be closer or faster than the flow up the thin side of the cookie, which could leave a dry backbone on top for longer.

Another observation is that gravity can help increase the flow velocity. Imagine we can somehow dip the cookie into an upside down cup. The gravitational pressure term is now in the same direction as the capillary term. This occurs for the top side of a cookie dipped slanted into a liquid. The soak front moves down faster than it moves upward, and the dry internal structure will be asymmetric.

Now solving for t by integration,

$$t = \frac{8\mu}{ r^2 \rho g \sin{\alpha}} X \left[ -\ln\left(1 - \frac{x}{X}\right) - \frac{x}{X} \right]$$

For small $\frac{x}{X}$ (the fraction of maximum distance), $ln(1-y) \approx -y-\frac{1}{2} y^2-\frac{1}{3} y^3-\cdots$

$$t \approx \frac{4\mu}{ r^2 \rho g \sin{\alpha}} X \left( \frac{x}{X}\right)^2$$

By substituting $X$ we recover the Washburn equation relating soak length to the time, pressure difference, surface tension, density, and viscosity:

$$x = \sqrt{\frac{\sigma r t \cos{\left(\theta\right)} } {2\mu} }$$

Or rearranging to solve for soak time

$$t = \frac{2\mu x^2}{\sigma r \cos{\left(\theta\right)}}$$

We can also incorporate a rough dependence on wetted area by noting that we are interested in the time to soak the volume and that

$$\frac{dx}{dt} A = \frac{dV}{dt}$$

With this we now have

$$t = \frac{2\mu x^2}{A \sigma r \cos{\left(\theta\right)}}$$

This simple equation has quite a bit of explanatory power. For the shortest soak time, we want large pores, low viscosity, short path lengths, low liquid contact angle (hydrophilic) and high surface tension. Note that the angle of the cookie is only contained in higher order terms, but $sin(\alpha)$ would be in the numerator so that a slanted dip (smaller angle $\alpha$) with the same wetted surface would reduce the soak time.

Warm tea vs cold milk

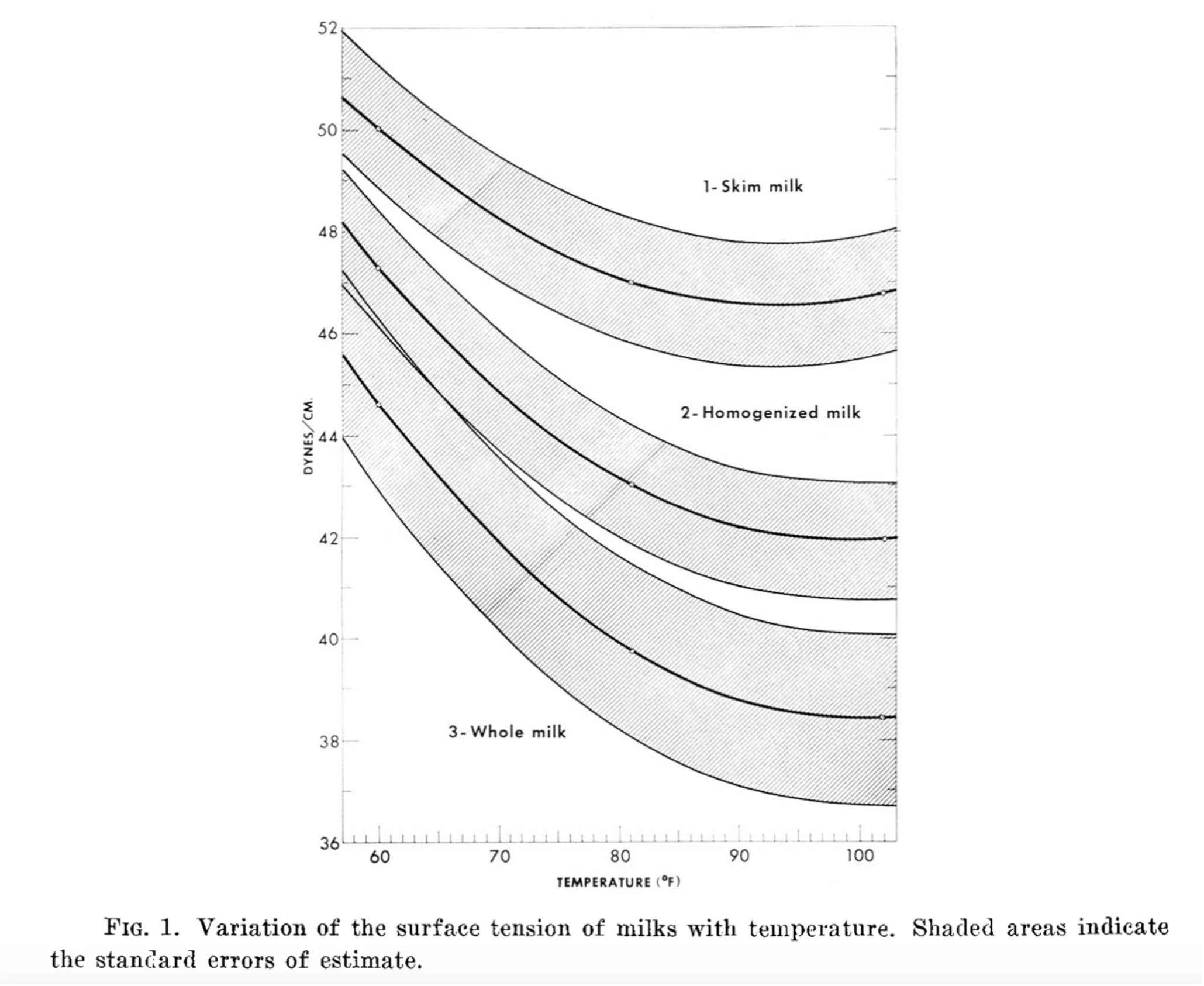
One observation we should be able to explain is that biscuits soak faster in tea compared to milk and the soak rate appears to slow down the more cookies have been dunked. This can be explained by viscosity. Water has a viscosity two times lower than milk, and its viscosity drops with increasing temperature (sidenote: cream has a viscosity about 15x greater than whole milk). So a hot mug of tea is going to soak a cookie much faster than a cold glass of milk. Similarly, the more cookies are dunked in a glass of milk, the more sugar is dissolved into the milk, which increases the viscosity and slows down the soaking.

Water’s higher surface tension also plays a role as the capillary pressure increases linearly with surface tension. Water’s surface tension against air is 72 dyn/cm ($1 \times 10^{-3}$) N·m) at 25°C and 58.9 dyn/cm at 100°C. Whole milk has a surface tension of 45.5 dyn/cm at 25°C and 35.5 dyn/cm at 100°C. This is another 1.5–2× factor ⁴.

I also suspect there's some differences in the liquid contact angle, and the chemistry and reaction rate of hot water dissolving sugars in the cookie, but not sure.

3 Milk surface tension.

The viscosity and surface tension of milk have interesting effects on splashing and droplet formation.

4 Milk drop tests Microscopy-UK.

Fully submerged cookies

I’ve also observed some dramatic variations in soak rate depending on the orientation and position of the cookie in the liquid. Here we are dealing with some subtleties about the cross-sectional flow area, imbibing length, pressure differences, and gas outlets.

One curious configuration is the fully submerged case. I'm aiming to maximize the flow area but the result is a cookie with that equilibrates with a dry internal section. To be clear - the cookie is fully submerged and is removed with a dry portion inside. What's happening? As fluid starts to permeate, where does the air that originally occupies the pores go? Some might manage to escape at the beginning, but it may be somewhat trapped because of the liquid boundary which seals the air inside unless its pressure is greater than the bubble point. I say somewhat because there may be a differential pressure that breaks the seal on the top. The internal pressure of the trapped air goes up, which opposes the capillary action or pressure difference that was driving the flow. This pressure must exceed the bubble point of the biscuit so that air can get through the pores on the cookie’s surface currently blocked by the liquid.

$$\Delta P_{\text{Bubble}} = \frac{2\sigma}{r}$$

The internal pressure also resists the capillary flow. The equilibrium between the two is reached when the fluid pressure equals the trapped gas pressure. The gas pressure starts to rise from $P_A$, the original atmospheric pressure, and it rises with the inverse volume. The fluid pressure driving the flow into the cookie is constant and is the sum of atmospheric, hydrostatic, and capillary pressure. This means the equilibrium is reached when the fluid occupies a fraction $\alpha$ of the total pore volume $V_p$.

$$\alpha = \frac{V_L}{V_p}, \quad \beta = \frac{V_g}{V_p}, \quad 1 = \alpha + \beta$$ $$P_{\text{gas}} = \frac{P_A}{\beta} = \frac{2\sigma}{R} + \rho g h + P_A$$ $$\alpha = 1 - \frac{P_A}{\dfrac{2\sigma}{R} + \rho g h + P_A} \approx 1 - \frac{P_A}{\dfrac{2\sigma}{R} + P_A}$$

I suppose the depths are often quite low, and the imbibing is not uniform, so there could be ways for a dominant gas path to establish itself and prevent a liquid seal. This could be aided by a pointy structure that concentrates the air flow in a small path with quickly rising high flow that does not get clogged by water. This could explain why this effect is not present in all cookies, just the most round and thick.

Something else to consider is that the gluten grains expand as they absorb water, which will lead to a shrinking pore size and kind of continuous exfoliation of the outer layer of imbibed cookie. This would probably be a kind of staggered process that would allow for instabilities and gas paths to form intermittently, relieving the pressure of the internal gas. If the pores were structurally sound, perhaps the capillary seal would work.

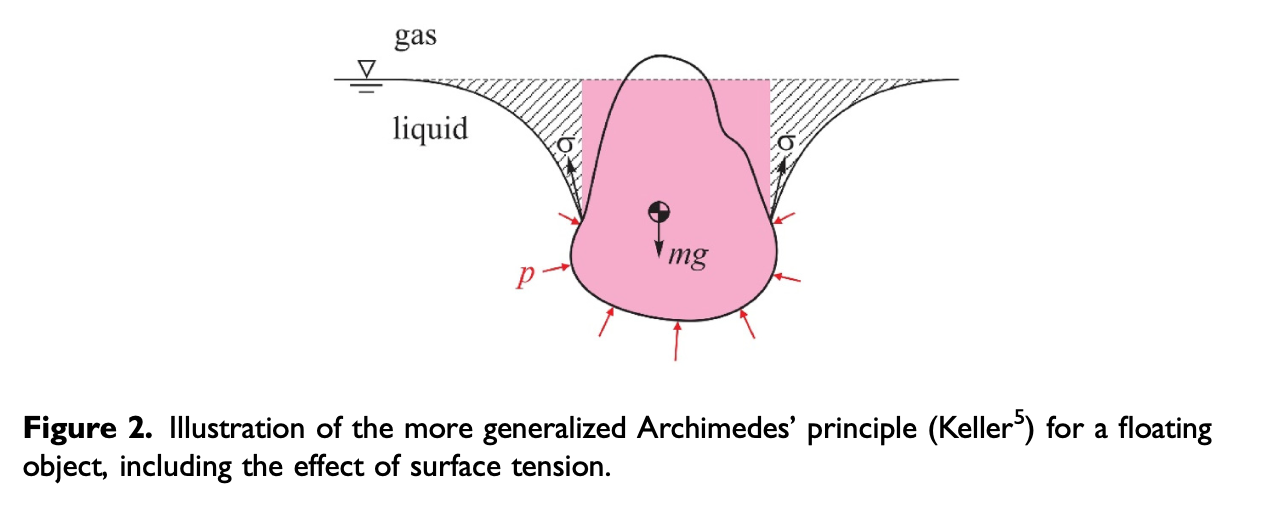
We can still maximize the surface area and minimize capillary path length by laying the cookie flat on the surface. Now this also has an unexpected result. The cookie soaks but never sinks! This is true when the top side is left dry at the start. If it is just slightly wetted it will soak and sink. But if it is dry, it remains afloat but fully soaked! It is however unstably afloat, because when you just touch, it sink right away. I believe this has to do with surface tension which helps create an upward force and an additional buoyancy force if the there is a below liquid level void created by the surface tension ⁵.

5 Generalized archimedes.

Next, I will introduce some new cookie geometries and properties that leverage these observations. There will be some new designs taking advantage of dynamic effects.

Footnotes

1. https://www.lenfisherscience.com/92-the-art-and-science-of-dunking/, 2015 ↩

2. Sman, Thermodynamic description of the chemical leavening in biscuits, 2021. ↩

3. Characterization Of The Pore Structure Of Starch Based Food Materials, 1992. ↩

4. Watson, Effect Of Variations In Fat And Temperature On The Surface Tension Of Various Milks, 1958. ↩

5. Naylor, Archimedes’ principle with surface tension effects in undergraduate fluid mechanics, 2022. ↩