_LCOE_thumb.png)
Design for Cost Methods
SpaceX's Falcon 9 is like a Toyota Corolla – an order of magnitude cheaper than competitor's "high performance" rocket systems, the Ferraris, but achieving the same basic transport requirements with greater reliability and safety. Before Falcon, space launch was a Ferrari-like industry, with handmade, highly specialized, extremely expensive vehicles targeting government customers and fully complicit in the inefficiencies of government contracting. Similarly, the nuclear industry produces and still designs Ferrari-like fission reactors, with high performance metrics in terms of power density and unit power, at a megaproject scale, but with high system and operational complexity, extreme development cost, numerous part counts, and very low production and deployment rates that still require human-machine interface to meet societal safety objectives. The demand for nuclear Ferraris in the U.S., particularly within non-traditional energy utilities is very low, as few competent utilities want unique reactors with such high capital costs, running at such high power that low probability accidents can have offsite consequences. Where is the nuclear Corolla?
_LCOE.png)
In the pursuit of energy systems that are cost effective and widely deployable, this thesis specifies a nuclear reactor architecture called the Class A HTGR (CA-HTGR), where Class A refers to the passive safety class during decay heat cooling. The architecture is used in a coupled design and cost approach to search for Levelized Cost of Electricity ( LCOE) minimizing designs. The feasibility and utility of this design for cost (DFC) methodology, also termed economics by design, is shown through assessment of advanced manufacturing opportunities and LCOE minimizing designs.
Section 1 introduces the history and status quo of fission energy, providing a perspective on the stalled industry and possible paths forward, motivated by the rapid expansion and success of the space launch industry. A comparison is made between nuclear and natural gas, suggesting possible cost reductions in a rebooted nuclear industry. Because of the unusual, black swan risk associated with nuclear, the starting point for massive cost reductions and widescale deployment is a new safety paradigm that reduces risk through consequence reduction. Through a technology description and down selection in Section 2, the CA-HTGR is shown to be the most effective architecture available for reducing consequence and mitigating hazards pertinent to nuclear fission reactors.
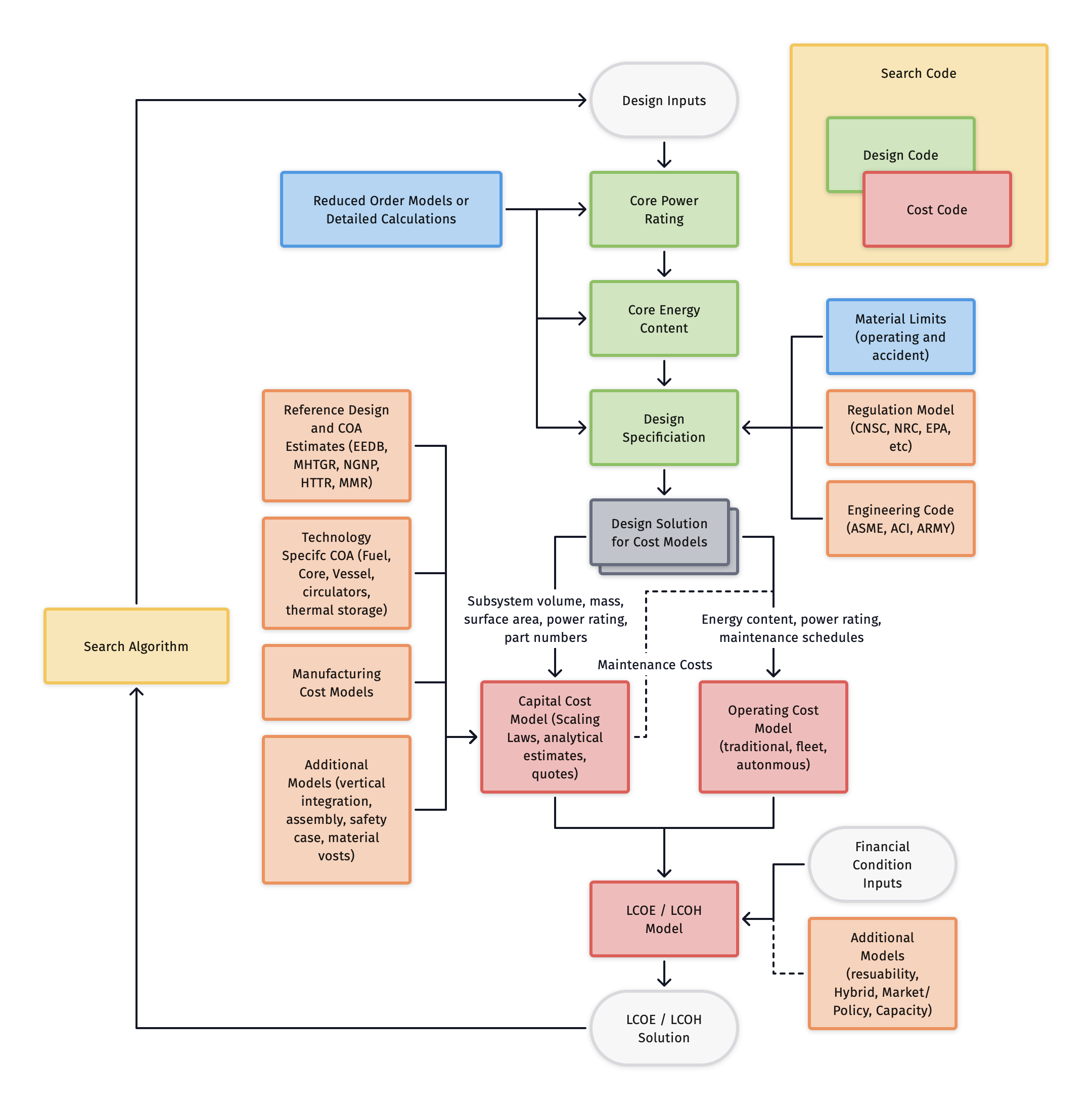
Nuclear reactor design has historically been a painful, one-off process with limited opportunity for optimization, iteration, and design exploration. Connections between design parameters and value functions like LCOE are often unclear or missing altogether. The wide-ranging disciplines, the timelines and development costs involved, and the barriers to change, combine to form a complex design process that often leads to siloed subsystem teams, and leaving little room for optimization, iteration, or integrated design, and more easily favors design by regulation, tradition, and sunk cost.
As an alternative to the traditional nuclear design approach, Section 2 introduces DFC methods made up of design, cost, and search codes. Instead of one-off labor-intensive estimates, DFC aims to automate estimates over a wide range of the design space with the end goal of LCOE minimization. Section 3 presents the design code and describes the models and assumptions used to specify an HTGR concept design, including models for core energy content, power rating, reactor vessel geometry, and balance of plant. Section 4 presents the cost code which includes estimates for CAPEX, OPEX, and project LCOE. Section 5 describes model uncertainty and design rankings, discussing the utility of each and possible methods for their estimation.
Advanced manufacturing (AM) and its potential use cases for nuclear fission are introduced in Section 6. DFC methods are used to evaluate the cost effects on an HTGR baseline. Rather than attempt detailed and high uncertainty cost estimation of advanced manufacturing methods, ranges of costs and performance factors were reported together with dependent LCOE changes. The results suggest various opportunities for AM and the utility of coupled design and cost estimation for evaluating the potential impacts of AM opportunities.
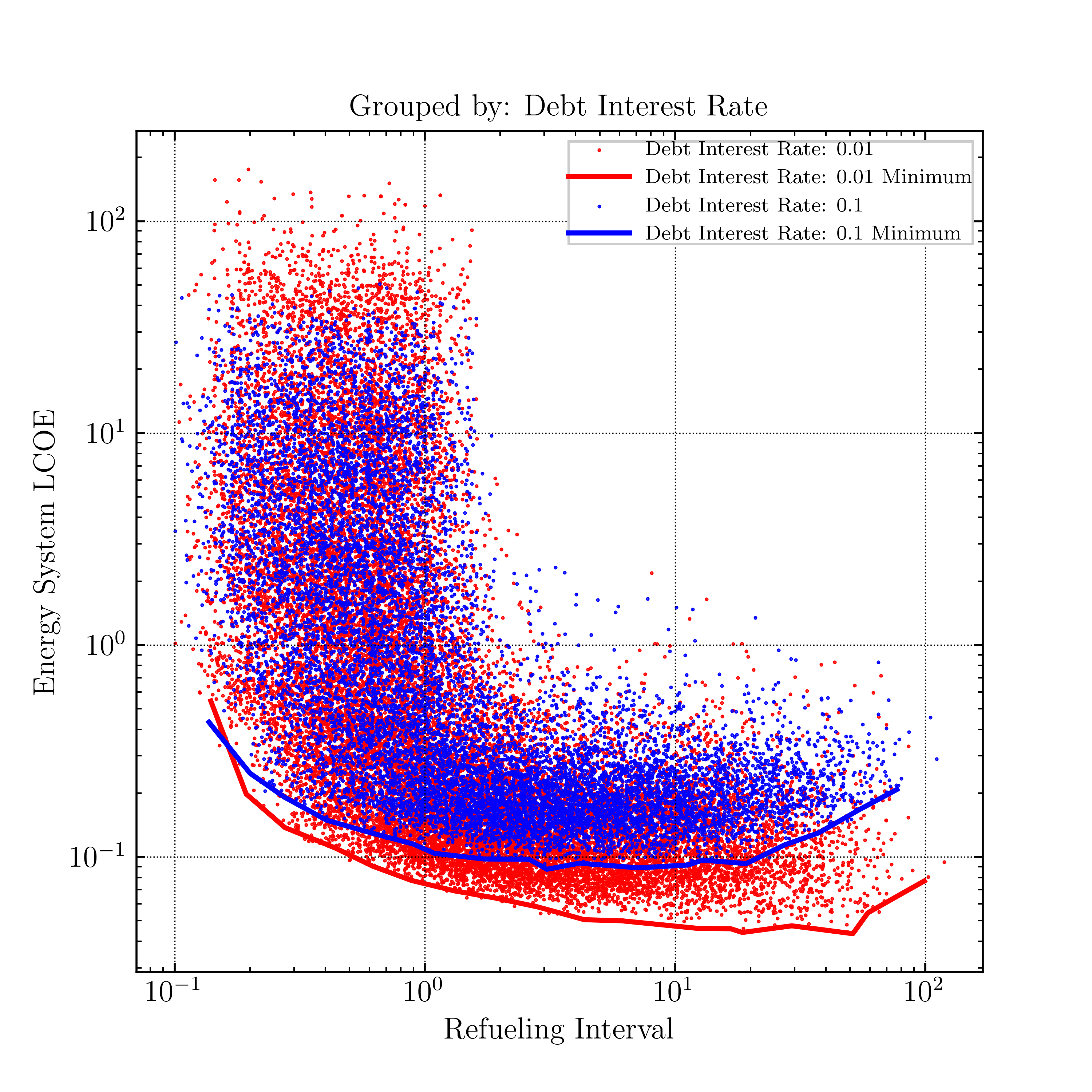
Finally, Section 7 presents the use of DFC methods to examine the design and cost space. A wide range of cost outcomes were found through random sampling of the design space. Genetic algorithms were used to search the design space for LCOE minimizing designs, establishing the feasibility of DFC methods for HTGRs.
The DFC methods developed and utilized for this thesis can be used to improve the delivery of cost competitive nuclear fission reactors for planet-wide deployment. DFC methods provide a system-focused approach that considers design interdependencies, allowing for optimization. The main shortcomings of the reported DFC methods include low fidelity design and cost approximations that may not match the reality of an HTGR. Optimizing on a simplified model can be useful because financial commitments are often made using similar or even simpler models. DFC methods could be used to quickly produce cost minimizing designs for a given population of end users and projects. In the future, nuclear projects can be accelerated by using DFC methods in conjunction with nuclear analysis codes, templating codes, and language models to automatically produce design and licensing documentation.
I'm open to applying similar methods to reactor architectures other than HTGRs, and taking a similar approach for other complex systems.